MATLAB
BÁSICO
Prof.
Alberto Adade Filho (ITA/CTA)
| 20. Traçando Gráficos no MATLAB |
| i. Introdução |
Os principais tipos de gráficos proporcionados são:
plot / plot3 : linear X-Y / linear X-Y-Z
loglog : log-log X-Y
semilogx / semilogy : semilog X-Y (eixo X logarítmico/eixo Y logarítmico, respectivamente)
polar : diagrama polar
mesh / surf : superfície malha tridimensional / superfície facetada tridimensional
stairs : próprio para sinais amostrados
hist, bar : histograma
| Obs. A saída gráfica é mostrada em janela(s) diferente(s) da janela de comandos. |
| ii. Forma Básica |
plot (Y) : produz um gráfico linear dos elementos do vetor Y pelos índices de Y. Se Y for uma matriz, é plotada uma curva para cada coluna de Y; o eixo x é rotulado de 1 a m, onde m é o número de linhas em Y.
Nesta forma básica, as escalas são estabelecidas automaticamente, bem como os eixos coordenados. Como é visto no exemplo a seguir, pode-se melhorar a saída dando-se título ao gráfico e rótulos aos eixos.
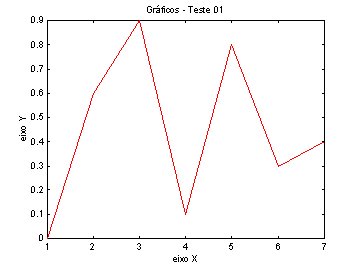
Ex.
y = [ 0 0.6 0.9 0.1 0.8 0.3 0.4];
plot(y)
title ('Gráficos - Teste 01')
xlabel ('eixo X')
ylabel ('eixo Y')

Dados dois vetores de mesma dimensão, x e y, pode-se traçar o gráfico de y versus x através do comando plot(x,y).
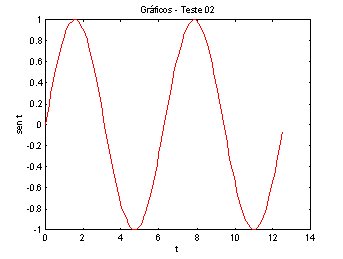
Ex.
t = 0 : .1 : 4*pi;
y = sin(t);
plot(t,y,'r')
title('Gráficos - Teste 02')
xlabel('t')
ylabel('sent')
Múltiplas curvas podem ser traçadas no mesmo gráfico com o comando,
plot (t1,y1,t2,y2,...,tn,yn)
que plota y1xt1, y2xt2, ..., ynxtn. Neste caso, t1, t2,...,tn podem ter tamanhos diferentes.
Ex.
t = 0 : .1 : 3*pi;
y = sin(t);
z=exp(-0.3*t) .* cos(t);
w = t .* sin(t);
plot(t,y, 'r',t,z, 'g',t,w, 'm')
xlabel('t', 'Color', 'b')
ylabel('Funções', 'Color', 'b')
title('Gráficos - Teste 03', 'Color', 'b')
text(2,0.8, 'SENO')
text(6,6, 't * SENO')
text(1,-1,'EXP * COSENO')

Neste exemplo são usadas diferentes cores para as curvas e os rótulos dos eixos e o título do gráfico são escolhidos na cor azul.
| Obs 1. O comando plot(x,Y), x vetor e Y matriz, plota as linhas ou colunas de Y versus x. A seleção de linhas ou colunas é feita em função do casamento com o número de elementos em x. Para Y quadrada, são plotadas as colunas de Y versus x. |
| Obs 2. O comando plot(X,Y), X e Y matrizes de mesma dimensão, plota as colunas de Y versus as colunas de X. |
| Obs 3. Quando o argumento para plot é complexo, a parte imaginária é ignorada exceto quando o argumento for único, onde então é plotada a parte real versus a parte imaginária. Portanto, plot(Z), Z matriz complexa, é equivalente a plot(real(Z),imag(Z)). |
| iii. Diagramas Polares |
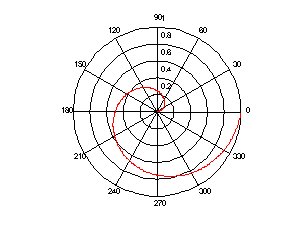
Ex 1. Traçar a função r = cos(2q ) num diagrama polar.
th = (pi/200 : pi/200 : 2*pi)' ;
r = cos(2*th);
polar(th,r) , grid

| Obs. 1 Usar o comando hold se houver necessidade de adicionar múltiplas curvas ao mesmo gráfico. |
| Obs. 2 Reticulado pode ser incluído e removido de um gráfico (grid on, grid off). |
Ex 2. Plotar a função R = k q , k = 1 / 2p , num diagrama polar.
R = th / (2*pi) ;
polar (th,R), grid
| iv. Curvas no Espaço Tridimensional |
plot3(x,y,z) : produz uma perspectiva (projeção bi-dimensional) da curva linear-por-partes que passa pelos pontos cujas coordenadas são os elementos de x, y e z, vetores de mesma dimensão.
Ex. Seja a curva parametrizada,
t = 0.01 : .05 : 10*pi;
x = cos(t); y = sin(t); z = t .^3;
plot3(x,y,z,'r')
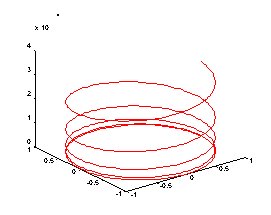
| Obs. O comando zlabel permite acrescentar um rótulo ao eixo z. |
| v. Particionamento da Tela |
A tela pode ser particionada em até quatro janelas, permitindo, deste modo, mostrar vários gráficos simultaneamente. O comando para isso é:
subplot(r,c,p)
A tela é particionada em r x c janelas e p é a janela atual. Por exemplo, subplot(2,1,2) particiona a tela em duas janelas na vertical e coloca o gráfico corrente na segunda janela.
Ex:
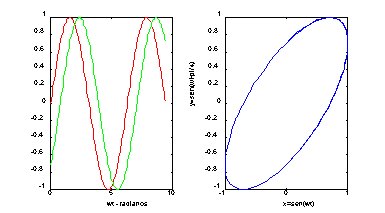
clf ; % limpa a tela gráfica
wt = 0 : 0.05 : 3*pi;
x = sin(wt);
y = sin(wt - pi/4);
subplot(1,2,1), plot(wt,x,'r',wt,y,'g'); xlabel('wt - radianos’)
subplot(1,2,2), plot (x,y,'b');
xlabel('x=sen(wt)'); ylabel('y=sen(wt-pi/4)')
| vi. Títulos, Rótulos, Texto, Grade |
title('Título','Propriedade1', 'Valor1', 'Propriedade2', 'Valor2')
xlabel('Rótulo do eixo-X','Propriedade1, 'Valor1')
ylabel('Rótulo do eixo-Y')
zlabel('Rótulo do eixo-Z')
grid : coloca reticulado no gráfico.
gtext('Texto para anotação'); % texto posicionado na tela pelo mouse
text(x,y,'Texto para anotação'); % coloca o texto na posição especificada por x e
% y, nas unidades do último gráfico
| vii. Controle de Tela e de Escalas |
shg : mostra a tela gráfica;
clf : limpa a tela gráfica;
hold on, (hold off) : mantém (ou não) o gráfico atual na tela tal que outros gráficos podem ser superpostos (nos mesmos eixos).
gcf : retorna o número da figura atual;
figure : abre uma nova janela para gráficos; figure(k) expõe a k-ésima figura e a torna a figura atual.
As escalas dos eixos são estabelecidas automaticamente. Para alterar o ajuste inicial assumido, usa-se o comando axis ([x_min,x_max,y_min,y_max]), em seguida ao comando plot. O comando axis sozinho retorna os limites dos eixos em uso; axis(‘auto’) propicia ajuste automático dos eixos; axis(axis) fixa os limites de eixos nos valores atuais; axis(‘equal’) estabelece incrementos iguais para os eixos; axis(‘normal’) restaura o padrão normal; axis(‘off’) apaga todos os rótulos e marcas dos eixos; axis(‘image’) ajusta "razão de aspecto" e limites dos eixos para representar imagens com pixels quadrados.
| Obs. Para gráficos tridimensionais:
axis([x_min, x_max, y_min, y_max, z_min, z_max]) |
| viii. Estilos de Linhas, Marcações e Cores |
O estilo da linha/símbolo utilizada na plotagem bem como a cor podem ser definidos através de um argumento para a função plot:
plot(x,y,S)
onde S é uma string de 1, 2 ou 3 caracteres (entre apóstrofos) construída a partir dos caracteres mostrados na tabela abaixo:
Símbolo |
Cor |
Símbolo |
Estilo da Linha |
y |
amarela |
· |
ponto |
m |
magenta |
° |
círculo |
c |
cyan |
x |
|
r |
vermelha |
+ |
|
g |
verde |
* |
asterisco |
b |
azul |
- |
linha cheia |
w |
branca |
: |
dois pontos |
k |
preta |
–· |
traço-ponto |
-- |
linha pontilhada |
| Obs. A ordem das cores conforme listadas na tabela acima é a seqüência pré-ajustada. Esta seqüência pode ser alterada modificando-se a propriedade ColorOrder (vide seção 20.xii). |
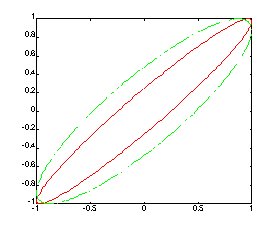
Ex.
t = 0 : pi/100 : 2*pi;
x = sin(t);
y1 = sin(t+0.25);
y2 = sin(t+0.5);
plot(x,y1, 'r-',x,y2, 'g--')
| ix. Gráficos de Superfícies |
mesh : mesh(v) cria uma perspectiva tridimensional dos elementos da matriz v. A superfície em malha, criada pelo comando mesh, é definida pelas coordenadas-Z (alturas) dos pontos acima de uma grade retangular no plano X-Y.
surf : semelhante à função mesh só que a superfície é sombreada.
Supor que se queira plotar z = f(x,y), onde x e y definem o domínio de f. Procede-se como segue:
1) Definir os vetores x e y em seus intervalos de valores;
2) Gerar um plano correspondente ao domínio. A superfície em malha é construída no topo deste plano com alturas determinadas pelos valores da função;
3) O comando meshgrid produz este plano criando duas matrizes com linhas e colunas repetidas dos vetores x e y;
4) Finalmente, a função é calculada nos elementos das matrizes resultantes. A função mesh (ou a função surf) é então aplicada sobre o resultado.
Ex 1. Plotar um gráfico de superfície do valor absoluto da função,
![]()
para -3 £ s £ 3 e -3 £ w £ 3.
w = linspace(-3,3,50); % cria vetor com 50 elementos linearmente espaçados %entre -3 e 3
s = linspace(-3,3,50);
[W,S] = meshgrid(w,s);
re = S .^2 - W .^2 + S + 1;
im = 2 * S .* W + W;
den = re + j * im;
g = 1 ./ abs(den);
mesh(s,w,g)
| Obs. 1 O ponto de visada do gráfico pode ser alterado através do comando view (azimute, elevação). |
| Obs. 2 waterfall(g) produziria um gráfico semelhante ao proporcionado pelo comando mesh acima, exceto que as linhas relativas às colunas não seriam traçadas no gráfico. |
Ex. 2.
n = 30; a = 1; r = 0.5;
teta = pi * (0 : 2 : 2 * n) / n;
fi = 2 * pi * (0 : 2 : n)' / n;
x = (a + r * cos(fi)) * cos(teta);
y = (a + r * cos(fi)) * sin(teta);
z = r * sin(fi) * ones(size(teta));
surf(x,y,z)
q = (a + r)/sqrt(2);
axis([-q,q,-q,q,-q,q])
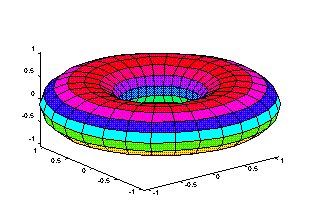
Nesses tipos de gráficos é utilizada a palheta (mapa) de cores vigente. A função colormap estabelece o mapa de cores a ser utilizado, alterando o ajuste predefinido. O comando help color lista os mapas de cores. No exemplo anterior o comando,
colormap(cool(6)); % estabelece uso do mapa de cores cool ( tons variados de %violeta e azul), em seis tonalidades, no caso.
alteraria as cores utilizadas no sombreamento das superfícies do toróide.
| Obs. Uma matriz definindo o mapa de cores tem dimensão nx3. Cada linha é interpretada como uma cor, onde o primeiro elemento especifica a intensidade de luz vermelha, o segundo, verde e o terceiro, azul. A intensidade da cor pode ser especificada no intervalo de 0 a 1. |
| x. Preparação de grades de dados e plotagem |
Para se produzir um gráfico de superfície (ou de níveis) de vetores x, y e z (z = f(x,y)), z deve ser mapeado para uma grade retangular x-y. Algumas vezes os dados não estão igualmente espaçados e a função de plotagem pode exigir isso (p. ex. contour). O exemplo a seguir mostra como se prepara grades de dados e como se gera dados igualmente espaçados, quando necessário. Basicamente faz-se uso da função griddata que interpola os dados permitindo gerar dados igualmente espaçados para fins de plotagem.
Ex. Sejam x, y, z vetores de dados espaçados de forma irregular:
x=[-1 -0.5 0. 0.2 0.8 1.4 1.7 2.5 3.5 4.0];
y=[-2 -1.2 -1.0 0 0.3 0.9 1.5 2.5 3.0 5.0];
z=[-1.5 -2.3 -1.1 0.5 1.9 3.5 2.0 0 4.8 3.1];
xmin=min(x); ymin=min(y); xmax=max(x); ymax=max(y);
xi=xmin:0.05*(xmax-xmin):xmax;
yi=ymin:0.05*(ymax-ymin):ymax;
zi = griddata(x,y,z,xi',yi); % preenche a grade definida por xi e yi interpolando % valores originais de x,y,z
contour(xi,yi,zi); % plota um gráfico de curvas de nível, tratando os valores de zi % como alturas acima de um plano definido por xi e yi.
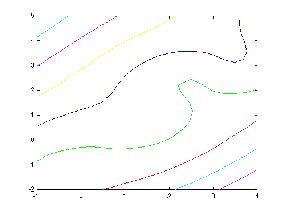
| Obs. A função contour (x,y,z) representa os valores de x e y que correspondem a um dado valor (nível) de z. |
| Obs. Valores de z podem ser colocados no gráfico usando-se o comando clabel (p. ex. cl = contour(xi,yi,zi); clabel(cl) ). |
No exemplo acima, alternativamente poder-se-ia utilizar o comando meshgrid para se gerar a nova grade igualmente espaçada:
x1 = linspace(min(x), max(x), 8); % define a grade X
y1 = linspace(min(y), max(y), 10); % define a grade Y
[xi,yi] = meshgrid(x1,y1); % produz a nova grade
zi=griddata(x,y,z,xi,yi)
contour(x1,y1,zi)
A saída de meshgrid está mostrada abaixo; note-se que as linhas de xi são iguais assim como as colunas de yi:
xi =
-1.0000 -0.2857 0.4286 1.1429 1.8571 2.5714 3.2857 4.0000
-1.0000 -0.2857 0.4286 1.1429 1.8571 2.5714 3.2857 4.0000
-1.0000 -0.2857 0.4286 1.1429 1.8571 2.5714 3.2857 4.0000
-1.0000 -0.2857 0.4286 1.1429 1.8571 2.5714 3.2857 4.0000
-1.0000 -0.2857 0.4286 1.1429 1.8571 2.5714 3.2857 4.0000
-1.0000 -0.2857 0.4286 1.1429 1.8571 2.5714 3.2857 4.0000
-1.0000 -0.2857 0.4286 1.1429 1.8571 2.5714 3.2857 4.0000
-1.0000 -0.2857 0.4286 1.1429 1.8571 2.5714 3.2857 4.0000
-1.0000 -0.2857 0.4286 1.1429 1.8571 2.5714 3.2857 4.0000
-1.0000 -0.2857 0.4286 1.1429 1.8571 2.5714 3.2857 4.0000
yi =
-2.0000 -2.0000 -2.0000 -2.0000 -2.0000 -2.0000 -2.0000 -2.0000
-1.2222 -1.2222 -1.2222 -1.2222 -1.2222 -1.2222 -1.2222 -1.2222
-0.4444 -0.4444 -0.4444 -0.4444 -0.4444 -0.4444 -0.4444 -0.4444
0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 0.3333 0.3333
1.1111 1.1111 1.1111 1.1111 1.1111 1.1111 1.1111 1.1111
1.8889 1.8889 1.8889 1.8889 1.8889 1.8889 1.8889 1.8889
2.6667 2.6667 2.6667 2.6667 2.6667 2.6667 2.6667 2.6667
3.4444 3.4444 3.4444 3.4444 3.4444 3.4444 3.4444 3.4444
4.2222 4.2222 4.2222 4.2222 4.2222 4.2222 4.2222 4.2222
5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000
A saída de griddata fornece,
zi =
-1.5000 -3.6231 -4.8905 -6.5450 -8.8930 -11.9982 -15.9128 -20.6776
-0.8296 -2.1962 -1.9195 -2.9614 -4.7177 -7.3370 -10.8129 -15.1359
1.2699 -0.1449 -0.2184 -0.2944 -1.3831 -3.6384 -6.7121 -10.5358
4.1305 2.1592 1.6928 2.2120 1.2276 -1.0675 -3.6772 -6.8095
7.3417 5.1846 4.1695 3.8075 2.0368 -0.1038 -1.6688 -3.7129
10.5542 7.8979 5.7431 3.5911 1.0790 -0.3326 0.0417 -0.6773
13.7236 10.5569 7.5749 4.6092 1.8257 0.7470 2.9854 2.6068
16.9728 13.5340 10.2637 7.2748 5.0308 4.4986 5.4081 4.2140
20.2952 16.7781 13.4694 10.5543 8.3386 7.0111 5.9422 3.8001
23.5479 20.0203 16.6766 13.6432 11.0167 8.6987 6.2321 3.1000
| xi Impressão de Gráficos |
O comando print faz uma cópia de alta resolução da tela gráfica para a impressora. Os valores predefinidos utilizados pelo comando print estão no M-file printopt.m; o usuário pode alterar tais valores editando este arquivo.
O comando,
print nome-do-arquivo
salva o gráfico corrente no arquivo especificado; se o arquivo especificado já existir ele é substituído pelo novo, a menos que seja usada a opção append:
print -append nome-do-arquivo
que acrescenta o gráfico corrente ao arquivo existente. Dessa forma, pode-se ter vários gráficos num mesmo arquivo.
A versão 4.2 proporciona o recurso de salvar e recarregar um gráfico. O comando,
print -dmfile nome-do-arquivo
cria um M-file contendo as informações necessárias para posteriormente reproduzir a figura. Esta versão também possibilita especificar que janela gráfica deve ser impressa, utilizando-se a opção -f. Por exemplo,
print -f2
imprime a janela de figura cujo handle (vide sub-seção xii) seja 2, qualquer que seja a janela de figura corrente. Um diagrama de blocos Simulink (software para simulação de sistemas dinâmicos, integrado ao Matlab) pode ser impresso usando-se o título da janela, por exemplo,
print -ftanques
onde tanques entitula a janela Simulink.
| Obs. Caso linhas e textos estejam aparecendo na cor preta embora especificadas diferentemente numa impressora colorida, alterar (editando) o arquivo printopt.m, colocando a opção -dwinc em vez de -dwin. |
Pode-se salvar figuras geradas no MATLAB em quatro formatos de modo que possam ser exportadas para outros programas baseados em Windows:
print -dbitmap nome-do arquivo % formato Windows Bitmaps (*.bmp)
print -dmeta nome-do-arquivo % formato Windows Metafile (*.wmf)
print -dhpgl nome-do-arquivo % formato HP Graphic Language (*.hgl)
print -deps nome-do-arquivo % formato Encapsulated Postscript (*.eps)
A opção Copy do menu Edit na janela da figura também pode ser usada para se transferir uma figura do MATLAB para outra aplicação Windows.
O formato PostScript é o que apresenta o melhor resultado gráfico mas uma impressora compatível com PostScript tem que ser usada e as figuras, uma vez criadas, não podem ser editadas. O formato HPGL pode ser lido por muitas aplicações não baseadas em Windows mas os arquivos gerados costumam ser muito grandes. O formato Bitmap é o que propicia menor resolução entre os formatos acima mas todas as cores são capturadas. O formato Windows Metafile é capaz de produzir gráficos de qualidade próxima a obtida no formato PostScript mas os arquivos só podem ser lidos por programas baseados no Windows.
| Obs. Na versão 4.2 em diante, como sugestões para exportar gráficos no formato Windows Metafile: (1) desabilitar a opção "Copy options: Honor Figure Properties", no menu Edit da janela da figura; (2) digitar o comando system_dependent(14,'on') antes de gerar a figura. |
| xii Manipulação de Gráficos |
Todo objeto gráfico tem um conjunto de propriedades (cor, tamanho, posição etc) associado a ele (e que pode ser especificado) no momento de sua criação. A cada objeto gráfico (figure, axes, line, text, patch, surface, image, uicontrol, uimenu) o MATLAB atribui um número denominado handle. Uma vez conhecido tal atributo, suas propriedades podem ser alteradas. Para se obter o handle de um gráfico, por exemplo, faz-se,
handle = plot(x,y)
Para se saber quais são as propriedades de um objeto gráfico e como alterá-las utiliza-se os comandos get e set. A sintaxe básica para esses comandos é como segue:
get (handle, ‘NomedaPropriedade’)
set(handle, ‘NomedaPropriedade’, ‘ValordaPropriedade’)
Para se determinar o valor de uma propriedade do objeto, utiliza-se o comando get como no exemplo: c = get(handle,’color’). O comando get sem se especificar as propriedades, get(handle), retorna uma lista com todas as propriedades e valores atuais para o objeto correspondente; por exemplo, get (gcf) determina as propriedades associadas com a figura atual (no caso a do exemplo de curvas de níveis) (vide tabela abaixo, lista à esquerda). Para se determinar as propriedades de um objeto que podem ser controladas pelo usuário, tecla-se set(handle). Os pré-ajustes (default) opcionais (isto é, aqueles que podem ser alterados) são mostrados entre chaves {}; por exemplo, set(gcf) retorna, para a figura em foco, a lista à direita,
get (gcf) |
set(gcf) |
| BackingStore
= on Color = [1 1 1] Colormap = [ (64 by 3) ] CurrentAxes = [0.000366211] CurrentCharacter = CurrentMenu = [1] CurrentObject = [1] CurrentPoint = [206 10] FixedColors = [
] InvertHardcopy = on |
BackingStore:
[ {on} | off ] Color Colormap CurrentAxes CurrentObject InvertHardcopy: [ on | {off} ] KeyPressFcn MenuBar: [ none | {figure} ] MinColormap Name NextPlot: [ new | {add} | replace ] NumberTitle: [ {on} | off ] PaperUnits: [ {inches} | centimeters | normalized | points ] PaperOrientation: [ {portrait} | landscape ] PaperPosition Pointer: [ crosshair | {arrow} | watch | topl | topr | botl | botr | circle | cross | fleur ] Position Units: [ inches | centimeters | normalized | points | {pixels} ] WindowButtonDownFcn |
Note-se que os valores válidos para BackingStore são on e off, com o valor predefinido sendo on; já Color não tem qualquer valor como propriedade uma vez que não há uma cor fixada para a figura, isto é, a cor pode ser qualquer vetor RGB válido. Algumas propriedades não apresentam valor predefinido. O comando getpref lista todas as propriedades que têm valor predefinido; alguns ajustes predefinidos são: LineColor, TextColor, TextFontSize, AxesAspectRatio, AxesLineWidth, FigureColor, FigurePosition e vários outros.
As seis últimas propriedades listadas (de ButtonDownFcn até Visible) são comuns a todos os objetos.
Uma tabela semelhante para as propriedades associadas aos eixos atuais está mostrada a seguir.
get(gca) |
set(gca) |
| AspectRatio = [NaN NaN] Box = on CLim = [0 1] CLimMode = auto Color = none CurrentPoint = [ (2 by 3) ] ColorOrder = [ (6 by 3) ] DrawMode = normal FontAngle = normal FontName = Helvetica FontSize = [12] FontStrikeThrough = off FontUnderline = off FontWeight = normal GridLineStyle = : LineStyleOrder = - LineWidth = [0.5] NextPlot = replace Position = [0.13 0.11 0.775 0.815] TickLength = [0.01 0.025] TickDir = in Title = [69.0001] Units = normalized View = [0 90] XColor = [1 1 1] XDir = normal Xform = [ (4 by 4) ] XGrid = off XLabel = [66.0001] XLim = [-1 4] XLimMode = manual XScale = linear XTick = [-1 0 1 2 3 4] XTickLabels =
XTickLabelMode = auto
YTickLabelMode = auto |
AspectRatio Box: [ on | {off} ] CLim CLimMode: [ {auto} | manual ] Color: [ {none} ] -or- a ColorSpec. ColorOrder DrawMode: [ {normal} | fast ] FontAngle: [ {normal} | italic | oblique ] FontName GridLineStyle: [ - | -- | {:} | -. ] |
Todos os objetos gráficos são armazenados hierarquicamente. Essa hierarquia pode ser inspecionada através das propriedades ‘parent’ e ‘children’. Vide Apêndice para uma listagem das propriedades dos objetos gráficos e MATLAB Reference Guide e MATLAB Release Notes para uma documentação mais completa a respeito deste assunto.
Seguem-se alguns exemplos de como alterar propriedades dos objetos.
O primeiro exemplo mostra como trocar a cor da linha em um gráfico; supor o gráfico gerado pela função fplot:
fplot(‘humps’, [0 2]); % gera gráfico da função humps
L1=fplot(‘humps’, [0 2]);
set (L1, ‘Color’, ‘r’); % troca a cor da linha do gráfico para vermelho.
Para se alterar a largura de linha,
set (h, ‘LineWidth’, size)
onde h é o identificador (handle) para uma linha e size é a largura que se deseja (pré-ajuste é de 0.5). Para se alterar a fonte usada nos rótulos dos eixos,
set (h, ‘FontName’, fonte)
Usando gca (de "get current axis") ou gcf (de "get current figure") como o handle no comando get ou set, pode-se alterar as propriedades dos eixos atuais ou da figura atual. Por exemplo, para se alterar o valor de pré-ajuste para as linhas de eixos,
set (gca, ‘LineWidth’, 10) % qualquer linha plotada a partir deste comando terá %uma largura de 10
Para se alterar para courier a fonte dos rótulos dos eixos antes de serem criados,
set (gca, ‘FontName’, ‘courier’)
Para se especificar um dos extremos de um eixo deixando o outro extremo ser auto-escalonado, p. ex. o limite mínimo do eixo-x em zero e o limite máximo auto-escalonado,
set(gca, 'XLim', [ 0 Inf ])
e o limite máximo em 40, deixando o limite mínimo ser auto-escalonado,
set(gca, 'XLim', [ -Inf 40])
Para se tornar invisíveis os eixos,
set (gca, ‘Visible’, ‘off’)
Para especificar que tipos de linhas e a ordem em que devem ser usadas, por exemplo,
set(gca, 'LyneStyleOrder', ' - | -- | : ')
Para alterar a cor do título do eixo atual para vermelho,
set(get(gca,'Title'), 'Color', 'r')
Para se estabelecer o pré-ajuste de cor dos eixos para a figura corrente,
set (gcf,’DefaultAxesColor’, [0 1 0])
Todos os eixos criados nesta janela de figura serão verdes; se alguma outra janela de figura for criada, a cor dos eixos voltará a ser a original. Para se estabelecer a cor verde como sendo a cor predefinida para os eixos das figuras para a sessão completa do MATLAB,
set (0,’DefaultAxesColor’, [0 1 0])
Para se alterar a ordem das cores no gráfico atual,
set(gca,'ColorOrder', [ 0 0 0])
O último argumento no comando acima é qualquer vetor RGB.
Para se alterar a cor de fundo de um gráfico de preto para branco, teclar cinvert. Para tornar branco o pré-ajuste, incluir uma linha no arquivo startup.m com o comando whitebg.
Para se alterar a cor da janela da figura para outra diferente de branca ou preta, p. ex. vermelha,
set (gcf, ‘Color’, ‘red’)
Para se ajustar o tipo do papel, por exemplo, para ‘A4’,
set (0,’DefaultFigurePaperType’, ‘A4’)
Após se alterar o valor de uma propriedade pode-se querer reverter este valor a uma situação anterior; para isso, usa-se uma das opções: default, factory ou remove no comando set. Por exemplo, preto é o valor original instalado para cor e supor que o valor de pré-ajuste tenha sido alterado para verde. Então,
set(gcf, ’Color’, ‘factory’) % torna a figura novamente preta
set(gcf, ‘Color’, ‘default’) % torna a figura novamente verde
Utiliza-se remove para se desistir de valores pré-ajustados pelo usuário; no exemplo,
set(0, ‘DefaultFigureColor’, ‘remove’) %remove a cor verde como pré-ajuste